Using GPT-5 to prove new theorems on matrix multiplication

This year i asked myself a question:

To put it into numbers, let's denote by $C(n, n, ... , n)$ the minimal number of multiplications needed to compute the product of $k$ matrices of size $n \times n$. Surprisingly there is no literature even on multiplication of 3 matrices, so nothing about $C(n, n, n)$ is known.

After spending a few days, I got a satisfying answer. But only with help of LLMs (o3 and GPT5).

Warmup: Multiplication of two matrices

If we have two matrices $A$ and $B$

The usual way to multiply them is to compute each of the 4 entries with formulas:

This way we need 8 multiplications and 4 additions. This should've been the end of the story. But in 1969, Volker Strassen discovered that 7 multiplications is possible:

This shows that $C(2, 2) \leq 7$. Soon after people proved that $C(2, 2) = 7$. Amazing property of this algorithm is non-commutativity: $a_i$ and $b_j$ don't need to be numbers. They can be $n\times n$ matrices themselves, and this shows that to multiply $2n \times 2n$ matrices, you can do 7 multiplications of $n \times n$. Therefore: $$C(2n, 2n) \leq 7 C(n, n) $$

With a bit of recursion magic, you get $$C(n, n) \leq 7^{\lceil \log n / \log 2 \rceil} \approx n^{\log_2 7}$$ this gives us an algorithm to multiply $n \times n$ matrices in $O(n^{\log_2 7}) \approx O(n^{2.807})$ operations, which is faster than the usual $O(n^3)$.

Strassen algorithm showed us that matrix multiplication complexity is not $O(n^{3})$, it can be reduced to $O(n^{2.807})$. The exact complexity remains a famous open problem in Computer Science. It is conjectured to be $O(n^2)$, but the best known complexity as of 2025 is $O(n^{2.3713})$. A lot of effort goes into changing this.

First Unknown Case: Three $2\times 2$ Matrices

What if we have three matrices to multiply?

The obvious way is to multiply the first two matrices $A \cdot B$ (7 multiplications using Strassen), and then multiply the result by the third matrix $(AB)\cdot C$ (another 7 multiplications with Strassen). This shows that $C(2, 2, 2) \leq 7 + 7$.

This seems like the best and only way, until you realize that we can also change the order: first compute $B\cdot C$ and then $A \cdot (BC)$. This shows that there are at least two algorithms with 14 multiplications that use completely different intermediate expressions. Then you realize that there are tons of algorithms in between: we can compute some expressions from the first ordering, some expressions from the second ordering, and mix them in some way to get the answer!

This is where you can try to come up with a better algorithm or prove that sequential algorithm is optimal. You will find that the algorithm space is huge and not well-behaved.

Defining algorithm space

To make the problem somewhat more tractable we impose very natural conditions on the algorithm space:

• Without divisions: we can only use additions, subtractions, and multiplications. For example, multiplying $(a_1 + a_2)$ by $\frac{1}{b_1 + b_2}$ is not allowed.
• Homogeneous in each matrix entries: each intermediate expression is homogeneous in variables from each matrix, meaning $a_1 b_2 + a_3$ and $a_1 b_1 + b_2 c_2$ are not allowed.
• Non-commutative: the order of multiplication matters, meaning $a_1b_1 \neq b_1a_1$.

The first two conditions are likely to hold true for optimal algorithm. But, strictly speaking, we don't know for sure. The non-commutativity condition allows algorithm to work for any matrix size $n$, just like Strassen.

Conversation with o3 discovers proof idea

If you ask o3 directly to find the minimal number of multiplications for our smallest case, it can't give any meaningful proof. It misunderstands the algorithm class. However, in discussion about algorithm class, o3 give a nice idea how to get obtain lower bounds. See o3 response here.

Prompt:

Let D = ABC be a product of three 2x2 matrices. Entries of D are trilinear expressions from R[A] \otimes R[B] \otimes R[C]. Let S_AB be the set of all bilinear expressions from R[A] \otimes R[B] and S_BC be the set of all bilinear expressions from R[B] \otimes R[C]. Let T_AB be rank-1 trilinear expressions obtained by considering all possible products t \otimes (sum gamma_i c_i), where t from S_AB. Let T_BC be rank-1 trilinear expressions obtained by considering all possible products (sum alpha_i a_i) \otimes k, where , where k from S_BC. Your goal is to find out whether all entries of D can be obtained as linear combinations of a single size 6 subset of T_AB \cup T_BC.

Key idea from o3 can be summarised as follows:

1. Write down the computation graph for $ABC$.
2. Specialize $C$ to be identity matrix $I$. Hence computation reduces to the product $AB$.
3. Consider tensor rank contributions in the computation graph. In total they compute $AB$ hence they must be at least $C(2, 2) = 7$.
4. Obtain lower bounds on $C(2, 2, 2)$

Visual explanation of the proof:

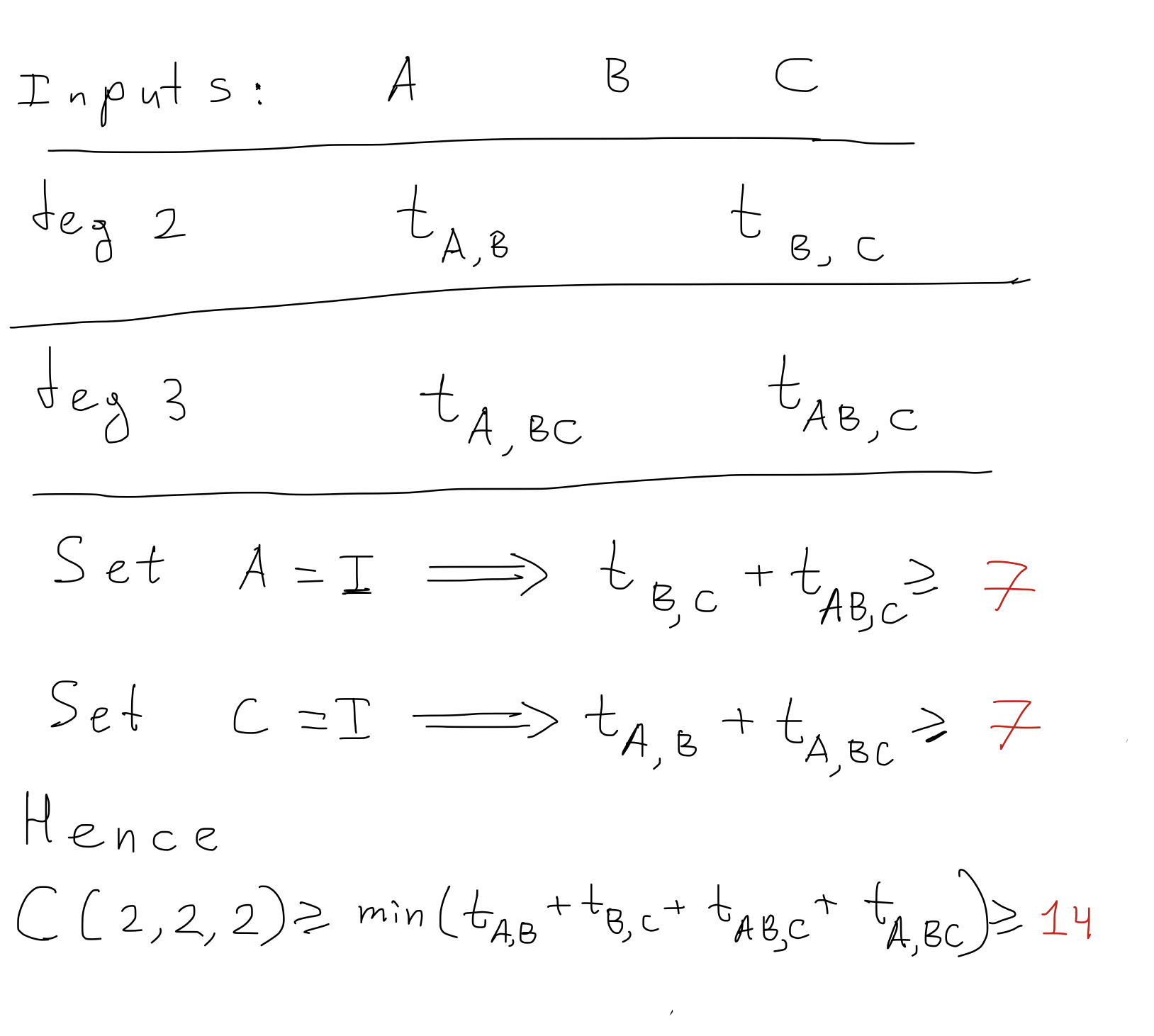
GPT-5 proves the general case

Prompt:

Let A_1, ..., A_k be n x n matrices. Consider the space of homogeneous non-commutative algorithms without division. Let M_{k}(n) be minimal number of multiplications necessary to multiply k of nxn matrices. Prove that M_{k}(n) = (k - 1) * M_{2}(n)

See the full response from GPT-5-Thinking here.

The proof can be summarized as follows:

1. Step 0: We consider homogeneous non-commutative arithmetic circuit without divisions that computes the product $A_1 ... A_k$. For an ordered tuple $S$, we denote by $M_{S}$ linear combination of monomials $\prod_{s \in S} a_{ij, s}$, where $a_{ij. s}$ is an entry of matrix $A_s$.
2. Step 1: We show that every multiplication in the circuit can be assumed to be a multiplication between elements from $M_{(p, p+1,...,r-1, r)}$ and $M_{(r+1,r + 2, ..., q-1, q)}$.
3. Step 2: We denote the number of such multiplications $t_{p, r, q}$. By specializing all matrices to $I$ except $A_r$ and $A_{r+1}$ we find that only multiplications counted by $t_{p, r, q}$ add contributions to the tensor rank of the result.
4. Step 3: Since the result is equal $A_r A_{r+1}$, its tensor rank must be at least $C(n, n)$. We get a bound $\sum_{p, q} t_{p, r, q} \geq C(n, n)$. Summing this over all $r$ gives $C(n, ..., n) \geq (k - 1)C(n, n)$.

Generalizations and beyond

It may be possible to drop some assumptions on algorithm class and still prove that sequential algorithm is optimal. It would be very interesting to see whether some commutative algorithms can be faster than sequential.

You can cite this blog:

@misc{Rybin2025,
    author = {Dmitry Rybin},
    title = {Using GPT-5 to prove new theorems on matrix multiplication},
    year = {2025},
    howpublished = {\url{https://rybindmitry.github.io/blogs/gpt5-matrix-multiplication.html}}
}